odehybrid | An Uncommon Lab

`odehybrid`

Hybrid continuous and discrete propagation.

This function propagates an ordinary differential equation along with a discrete update equation in a manner similar to MATLAB's ode45 function (which only propagates an ordinary differential equation). This is useful for implementing discrete-time controllers or simulating processes that are updated at discrete intervals.

Interfaces

[t, yc, td, yd] = odehybrid(solver, ode, ...
                            de, dt, ...
                            ts, ...
                            yc0, yd0);
                            
[t, yc1..m, td, yd1..n] = odehybrid(solver, ode, ...
                                    de, dt, ...
                                    ts, ...
                                    {yc1, yc2..m}, {yd1, yd2..n});
                                    
[t, ..., td, ..., te, yc1..m, yd1..n, ie] = odehybrid(solver, ode, ...
                                                      de, dt, ...
                                                      ts, ...
                                                      yc0, yd0);
                                                      
[...] = odehybrid(solver, ode, ...
                  {de1, de2, ...}, [dt1, dt2, ...], ...
                  ts, ...
                  yc0, yd0);
                  
[...] = odehybrid(..., [options], [log]);

sol = odehybrid(...);

Inputs

solver	Continuous-time propagator to use, e.g. `@ode45`
ode	Ordinary differential equation to use with solver. The interface should be `fun(t, xc1, xc2, ..., xcm, xd1, xd2, ..., xdn)` where `xc1, xc2, ..., xcm` are the continuous states and `xd1, xd2, ..., xdn` are the discrete states. It should return the derivatives of the continuous states (m outputs).
de	Discrete update equation(s) (either a function handle or cell array of function handles) with the same inputs as ode but outputing the updated continuous and discrete states (n+m outputs).
dt	Time step(s) of discrete update equation(s). If de is a cell array of multiple functions, this should be an array of the same size.
ts	Time span, `[t_start, t_end]`
yc0	Cell array of initial continuous states
yd0	Cell array of initial discrete states
options	(Optional) options structure from odeset
log	(Optional) `TimeSeriesLogger` for logging in the `ode` and `de`. If a log is passed in, both ode and de must be able to accomodate having a log input or not as the final argument. E.g., `ode` will be called as: `ode(t, xc1, ..., xd1, ..., xdn)` and `ode(t, xc1, ..., xd1, ..., xdn, log)`

Outputs

t	Times corresponding to continuous states (nc-by-1)
yc1, yc2, ... ycm	Continuous state outputs (m outputs, each nc-by-1)
td	Times corresponding to discrete state updates (nd-by-1)
yd1, yd2, ... ydn	Discrete state outputs (n outputs, each nd-by-1)
te	Times corresponding to events (ne-by-1)
yce1..m	Continuous states at events (m outputs, each ne-by-1)
yde1..n	Discrete states at events (n outputs, each ne-by-1)
ie	Index of triggering event. See documentation in odeset for more on events.
sol	If a single output is requested, it will be a structure with fields for each of the individual outputs. The various continuous states will be grouped in `yc`, the discrete into `yd`, the continuous states at events into `yce`, and the discrete states at events into `yde`.

Example

This is a quick example of simulating an unstable continuous system with a stabilizing discrete-time controller.

ode = @(t, x, u) [0 1; 2 0] * x + [0; 1] * u;  % Differential equation
de  = @(t, x, u) deal(x, -[8 4] * x);          % Discrete update equation
dt  = 0.1;                                     % Discrete eq. time step
ts  = [0 5];                                   % From 0 to 5s
x0  = [1; 0];                                  % Initial continuous state
u0  = 0;                                       % Initial discrete state
[t, x, tu, u] = odehybrid(@rkadapt, ode, de, dt, ts, x0, u0); % Simulate!
plot(t, x, tu, u, '.'); xlabel('Time');                       % Plot 'em.
legend('x_1', 'x_2', 'u');                                    % Label 'em.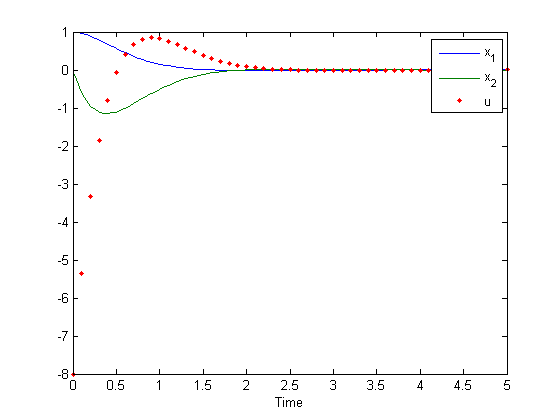

Docs

`odehybrid`

Interfaces

Inputs

Outputs

Example

See Also