rk4
Runge-Kutta 4th order integration method.
Implements numerical propagation of an ordinary differential equation from some initial value over the desired range. This function is similar to MATLAB's variable-step ODE propagators (e.g., ode45), but uses a fixed step method. This is useful either when one knows an appropriate step size or when a process is interrupted frequently (ode45 and the similar functions in MATLAB will always make at least a certain number of steps between ts(1) and ts(2), which may be very many more than are necessary).
[t, x] = rk4(ode, ts, x0, dt);
[t, x] = rk4(ode, ts, x0, options);
Inputs
| ode | Ordinary differential equation function |
|---|---|
| ts | Time span, [t_start, t_end] |
| x0 | Initial state (column vector) |
| dt | Time step |
| options | Alternately, one can specify an options structure instead of dt so that this function is compatible with ode45 and its ilk. The only valid fields are MaxStep (the time step) and OutputFcn |
Outputs
| t | Time history |
|---|---|
| x | State history, with each row containing the state corresponding to the time in the same row of t. |
Example
Simulate an undamped harmonic oscillator for 10s with a 0.1s time step,
starting from an initial state of [1; 0].
ode = @(t, x) [-x(2); x(1)];
[t, x] = rk4(ode, [0 10], [1; 0], 0.1);
plot(t, x);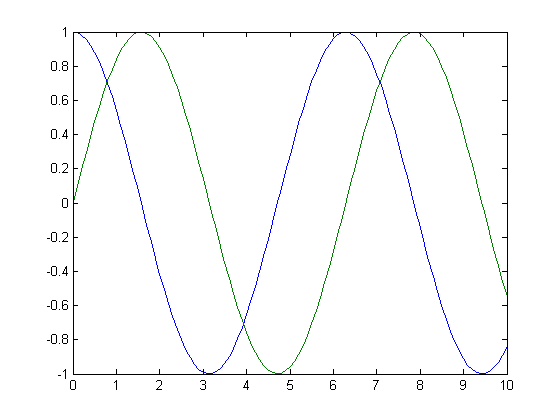
See Also
Solvers,odehybrid, rkadapt, rkfixed, ode45 (MATLAB)January 17th, 2025
©2025 An Uncommon Lab