Engine

The *kf algorithm generation engine combines a set of filter architectures and filtering ideas with a user's problem description to intelligently generate high-quality filtering algorithms.

It start with selecting the filter archiecture:

Linear & extended filters, with options for:

Extended (nonlinear) filters
Constant, input, and state-dependent noise covariance matrices and Jacobians
Covariance matrices, information matrices, and square-root forms
Iteration and backwards smoothing
Consider covariance
Sequential (scalar) updates
Flexible sensor update rates

Unscented filters

Nonlinear vs. additive process and measurement noise
Constant, input, and state-dependent noise covariance matrices
Covariance matrices and square-root covariance forms
Consider covariance
Flexible sensor update rates

Particle Filters

A user selects among these options and provides information about the dynamics and observation functions, noise terms, Jacobians, etc. The engine combines these for an efficient custom filter and generates the approriate code, whether as efficient MATLAB or C code.

The engine contains a set of tools for:

Generating an example simulation of the filter
Generating a Monte-Carlo wrapper for the simulation to determine if the predicted error covariance matches the true error covariance
Generating interfaces for the code, such as MEX files and Simulink blocks

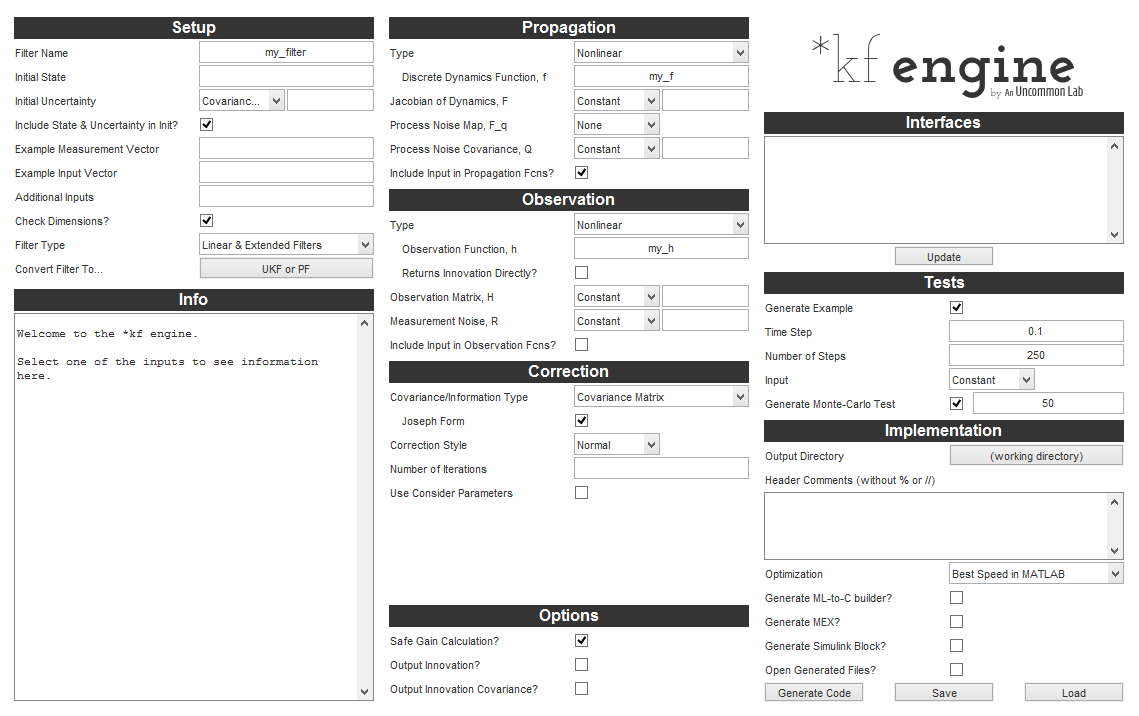
The engine is wrapped with a graphical user interface, exposing all of the applicable options to the user as architectures and options change. The interface is not necessary to use the engine (it can be invoked with a struct), but for the sake of this documentation, the engine and interface will always be described together.

Launching the Interface

The interface can be brought up at any time.

>> skfengine;

Filter Initialization and Step

When a filter is generated, it will consist of an initialization function and a function to call on each step, e.g.:

% Initialize
[x, P, constants] = my_filter_init();

% For each sample...
for k = 2:n

  % Run the filter.
  [x, P] = my_filter(t(k-1), t(k), x, P, z(:, k), constants);
  
end

where z(:, k) is the observation vector at time t(k).

Note that the filter has no internal state (it is reentrant); it simply processes based on the inputs. Therefore, we could use multiple filters at once or manually change the state estimate or information at any point with worrying about adverse effects.

Sections

The engine is broken into several sections to keep things tidy.

Setup

This consists of setting the name of the filter, the initial conditions, and the overall architecture of the filter.

Info

This box displays help about the selected field. It updates when the user changes something or right-clicks on a field.

Filter Options

These options change for each filter architecture and consist of things like inputs for the observation function, whether consider covariance should be used, if it's desirable to output the innovation vector, etc.

Interfaces

When the filter is generated, it will expect to call several of the user's functions, such as the propagation function. When the user clicks "Update" or "Generate", this box will update with the interfaces expected, using shorthand variable names described in nomenclature.

Tests

This box controls how the example simulation and Monte-Carlo test are generated, such as what time step and input to use and how many runs are desired.

Implementation

This box controls what type of code is generated and how it is wrapped, such as selecting C code for implementation with a Simulink block wrapper.

Next Steps

See setup next.

Docs