by An Uncommon Lab

Getting Started

What is *kf?

*kf is a tool that generates custom filters and also has a bunch of standard filters and utilities built in.

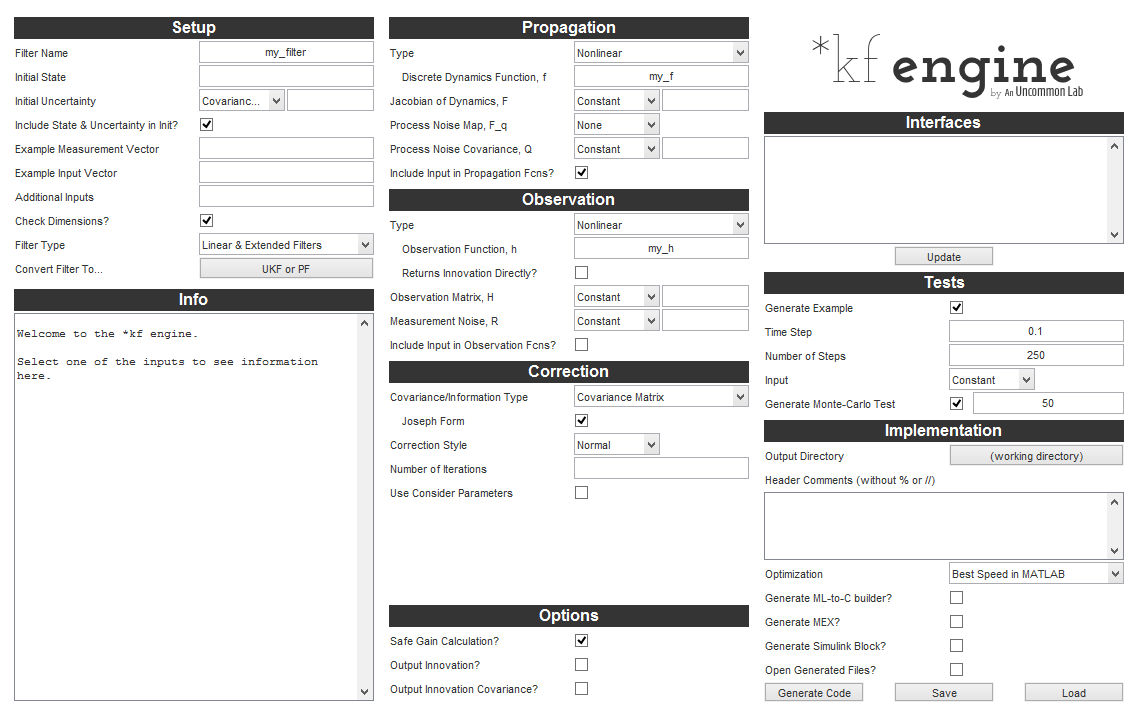
To generate a filter, we use the *kf engine, describe our problem to it (for instance, we say, “My propagation function is called propagate_the_state.m.”), select some filter options, and click Generate. It will write out some code that we can now run to filter at each time step. Looks something like this:

To instead use the built-in filters, we just call them as regular functions. The complex ones take some options. Using them generally looks something like this:

% Run a generic extended information filter for one sample.
[x_k, I_k] = eif(t_km1, t_k, x_km1, I_km1, u, z, f, invF, G, invQ, h, H, invR);

The above runs a single step of a generic extended information filter, updating a state estimate from x_km1 (“k-1”) to x_k. Sure, there are a lot of little inputs, but they're perfectly normal variables for an information filter. That's not so bad, right? So let's take a look at a more complex function, like kff, which can act like a regular discrete Kalman filter, an iterated filter, a Schmidt-type filter, or permutations of these ideas.

% Set the Kalman filter framework options
options = kffoptions(...);
 
% Call the Kalman filter framework for each measurement.
for k = 2:n
    ...
    [x_k, P_k] = kff(t(k-1), t(k), x_km1, P_km1, u_k, z_k, options);
    ...
end

Basically, the only difference is that these more complex functions, which we call framework functions, generally take in some additional options, which configure what the filter is suppose to do/use.

What about those utilities we mentioned? There are numerous, and you'll see them in the menu on the left towards the bottom. Here's a commonly useful function called normerr, which calculates statistical properties associated with estimation errors over time and corresponding covariance matrices:

normerr(x_true - x_estimated, P, 0.95);

That will plot the theoretical 95% confidence bounds on the errors given the covariance matrices in P along with the actual 95% error bounds.

Custom, Framework, or Basic Filter?

So which approach to filtering should you take? It depends on your needs. Let's start with the easiest.

If your runtime doesn't matter and you only need the most common filter types, like a generic unscented Kalman filter, then basic filters are a good place to start. These are the filters you can “just call” with your inputs.

If you need a little more advanced options, such as iteration, then frameworks are a good idea. Also, in cases where a framework exists, a basic filter might not exist, because their interfaces will be almost the same. For instance, there's no basic filter for an extended Kalman filter, because it would be just like the framework implementation of an extended Kalman filter. Basically, frameworks are just as easy to use as basic filters, but much more powerful.

If you need fast runtime, the most stable filter, code you can read, advanced options, or to eventually generate C code, custom filters via the *kf engine are the way to go. They take a little time to set up, but are generally better in every way than the generic filters.

Next Steps

To see what *kf is all about and see the custom filter engine in action, head over to the pendulum tutorial.

To see a tutorial for the Kalman filter framework, kff, take a look at the Eustace tutorial.

For examples of using the basic filters, click on any of the links under Basic Filters on the left. Each has a working example. In fact, the examples all use the same linear problem, so their performance and code can be directly compared. The unscented Kalman filter is a good place to start.

To skip the tutorials and learn more about the engine, see the engine page.

If you'd rather spend some time thinking about the right way to design and test filters, see the discussion of workflow.